√99以上 立体 面積 276457

体積の求め方 計算公式一覧
立体は円柱になり,表面積は底面積×2=16 π ×2 (cm 2 )と側面積8 π ×7 (cm 2 )の合計になります 底面積2つで32 π (cm 2 ),側面積56 π (cm 2 )の合計は π (cm 2 ) (答) ※以下,8番以後の問題を解くには,中学校3年生で習う三平方の定理が必要になります.まだ習っ47 7 立体の体積と表面積 133 次の図の直方体の体積と表面積を求めよ。 ⑴ ⑵ ⑶ 137 次の図の立体の体積と表面積を求めよ。 ⑴ ⑵ 135 次の図の円柱の体積と表面積を求めよ。 ⑴ ⑵ ⑶ 134 右 の図は ,円柱とその展開図である。 次の問いに答えよ。
立体 面積
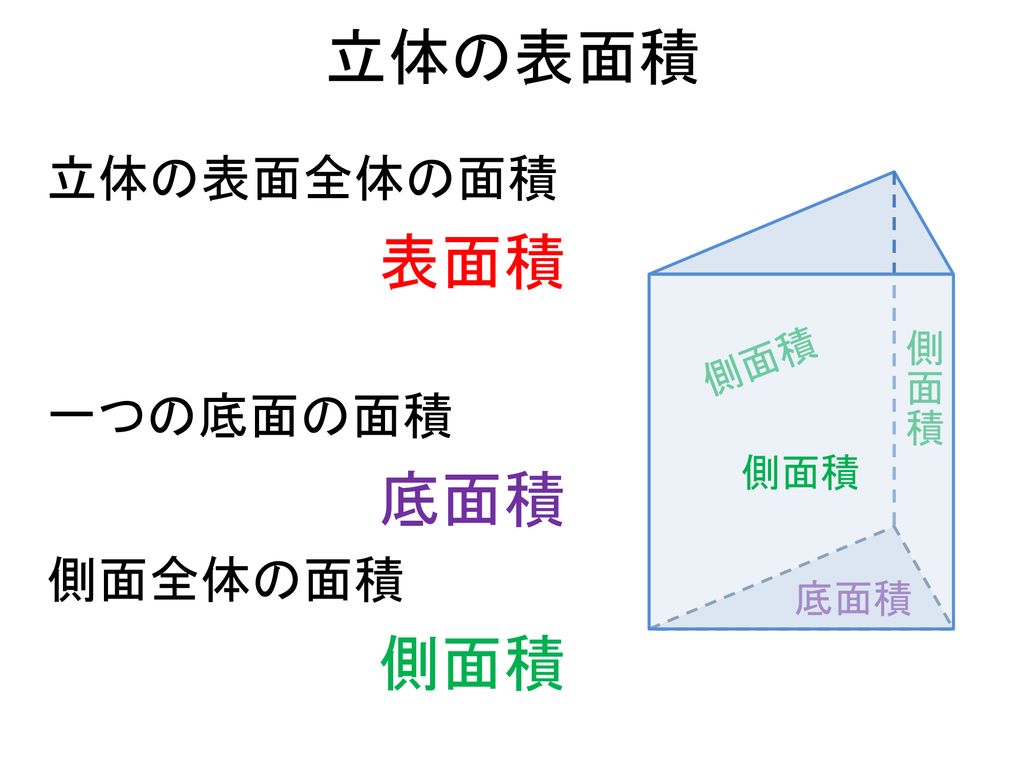
立体 面積- 立体を切り開いた図のこと ・柱体の表面積 底面積×2+側面積 (側面積=柱体の高さ×底面の周りの長さ) ・角錐の表面積 底面積+側面積 (側面積=合同な二等辺三角形×4) ・円錐の側面のおうぎ形の中心角 半 径 母 線 360 × 半 径 母 線 立体の表面積の求め方 立体の表面積とは 立体の表面全体の面積のこと をいいます。 立体の表面積の公式も一応示しますが、考え方を理解することができていればわざわざ公式を覚える必要はありません。
長さ 面積 体積 後編 立体 硫化鉄の 数学 を 数楽 にするブログ 楽しくドヤ顔で100点とる方法
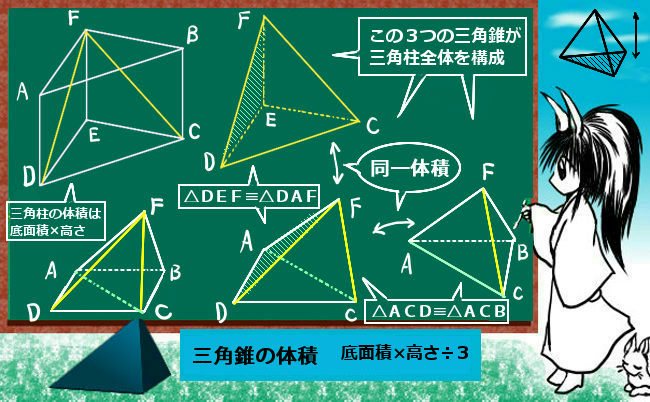
(ウ) 見付け面積の2分の1以上が窓であること。 サ 機械式駐車場 吊上式自動車車庫、機械式立体自動車車庫等で、床として認識することが困難な形状の部分について は、1台につき15㎡を、床面積として算 先がとんがった立体の体積は最後に3でわる っておぼえておこう。 まとめ:三角錐の体積の求め方の公式は3ステップ! 三角錐の体積の求め方をマスターしたね。 ようは、 底面積をだして、 高さをかけて、 最後に「3」でわればいいんだ。 体積・表面積 算数 中学数学 空間図形 立体の 体積の求め方(公式) を一覧にまとめました。 公式を忘れてしまったときには、こちらで確認しましょう。 体積の求め方公式 立方体・直方体の体積の求め方 円柱の体積の求め方 三角柱の体積の求め
その球帯面積は積分すれば、②のようになる。 ついでに球帽の面積と立体角の場合も示す。 その面積と立体角は③のようになる。 ()追記。 この立体角を使ったのは、電気工学の一つの分野である『電熱・照明』であった。 平行四辺形の面積は、 「面積 底辺 高さ」 「 面 積 = 底 辺 × 高 さ 」 で求められます。 たとえば、「底辺 4 c m ,高さ 3 c m の平行四辺形」の面積は 4 × 3 = 12 c m 2 となります。 これは、平行四辺形の右端の直角三角形を切り取って左側に移すと 「たて 3 c m立体角は、半径1の球(単位球)の一部の面積で定義されていました。単位球の表面積は $4\pi$ なので、立体角は、$0$ 以上 $4\pi$ 以下です。 「$4\pi$ ステラジアン」は「全方位」に対応する立体角です。 立体角の計算例
立体 面積のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 立体の体積まとめ 角柱 円柱 角錐 円錐 球 A 教遊者 |  立体の体積まとめ 角柱 円柱 角錐 円錐 球 A 教遊者 |  立体の体積まとめ 角柱 円柱 角錐 円錐 球 A 教遊者 |
立体の体積まとめ 角柱 円柱 角錐 円錐 球 A 教遊者 |  立体の体積まとめ 角柱 円柱 角錐 円錐 球 A 教遊者 |  立体の体積まとめ 角柱 円柱 角錐 円錐 球 A 教遊者 |
 立体の体積まとめ 角柱 円柱 角錐 円錐 球 A 教遊者 | 立体の体積まとめ 角柱 円柱 角錐 円錐 球 A 教遊者 | 立体の体積まとめ 角柱 円柱 角錐 円錐 球 A 教遊者 |
「立体 面積」の画像ギャラリー、詳細は各画像をクリックしてください。
 立体の体積まとめ 角柱 円柱 角錐 円錐 球 A 教遊者 |  立体の体積まとめ 角柱 円柱 角錐 円錐 球 A 教遊者 |  立体の体積まとめ 角柱 円柱 角錐 円錐 球 A 教遊者 |
 立体の体積まとめ 角柱 円柱 角錐 円錐 球 A 教遊者 |  立体の体積まとめ 角柱 円柱 角錐 円錐 球 A 教遊者 | 立体の体積まとめ 角柱 円柱 角錐 円錐 球 A 教遊者 |
 立体の体積まとめ 角柱 円柱 角錐 円錐 球 A 教遊者 |  立体の体積まとめ 角柱 円柱 角錐 円錐 球 A 教遊者 | 立体の体積まとめ 角柱 円柱 角錐 円錐 球 A 教遊者 |
「立体 面積」の画像ギャラリー、詳細は各画像をクリックしてください。
立体の体積まとめ 角柱 円柱 角錐 円錐 球 A 教遊者 |  立体の体積まとめ 角柱 円柱 角錐 円錐 球 A 教遊者 | 立体の体積まとめ 角柱 円柱 角錐 円錐 球 A 教遊者 |
 立体の体積まとめ 角柱 円柱 角錐 円錐 球 A 教遊者 |  立体の体積まとめ 角柱 円柱 角錐 円錐 球 A 教遊者 |  立体の体積まとめ 角柱 円柱 角錐 円錐 球 A 教遊者 |
 立体の体積まとめ 角柱 円柱 角錐 円錐 球 A 教遊者 |  立体の体積まとめ 角柱 円柱 角錐 円錐 球 A 教遊者 | 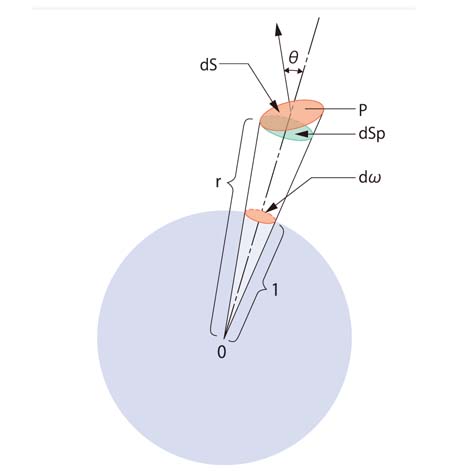 立体の体積まとめ 角柱 円柱 角錐 円錐 球 A 教遊者 |
「立体 面積」の画像ギャラリー、詳細は各画像をクリックしてください。
 立体の体積まとめ 角柱 円柱 角錐 円錐 球 A 教遊者 |  立体の体積まとめ 角柱 円柱 角錐 円錐 球 A 教遊者 | 立体の体積まとめ 角柱 円柱 角錐 円錐 球 A 教遊者 |
 立体の体積まとめ 角柱 円柱 角錐 円錐 球 A 教遊者 |  立体の体積まとめ 角柱 円柱 角錐 円錐 球 A 教遊者 | 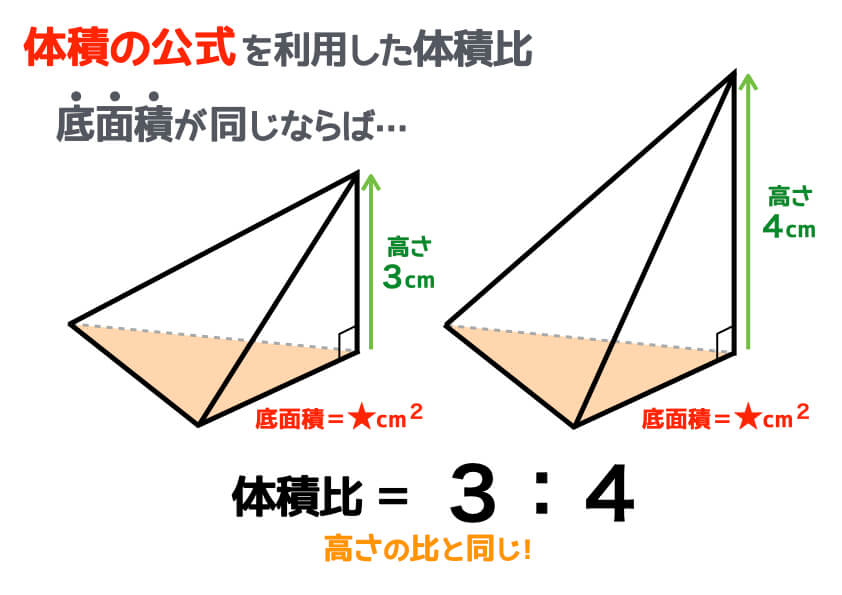 立体の体積まとめ 角柱 円柱 角錐 円錐 球 A 教遊者 |
 立体の体積まとめ 角柱 円柱 角錐 円錐 球 A 教遊者 |  立体の体積まとめ 角柱 円柱 角錐 円錐 球 A 教遊者 |  立体の体積まとめ 角柱 円柱 角錐 円錐 球 A 教遊者 |
「立体 面積」の画像ギャラリー、詳細は各画像をクリックしてください。
 立体の体積まとめ 角柱 円柱 角錐 円錐 球 A 教遊者 |  立体の体積まとめ 角柱 円柱 角錐 円錐 球 A 教遊者 |  立体の体積まとめ 角柱 円柱 角錐 円錐 球 A 教遊者 |
 立体の体積まとめ 角柱 円柱 角錐 円錐 球 A 教遊者 |  立体の体積まとめ 角柱 円柱 角錐 円錐 球 A 教遊者 |  立体の体積まとめ 角柱 円柱 角錐 円錐 球 A 教遊者 |
 立体の体積まとめ 角柱 円柱 角錐 円錐 球 A 教遊者 |  立体の体積まとめ 角柱 円柱 角錐 円錐 球 A 教遊者 |  立体の体積まとめ 角柱 円柱 角錐 円錐 球 A 教遊者 |
「立体 面積」の画像ギャラリー、詳細は各画像をクリックしてください。
 立体の体積まとめ 角柱 円柱 角錐 円錐 球 A 教遊者 | 立体の体積まとめ 角柱 円柱 角錐 円錐 球 A 教遊者 |  立体の体積まとめ 角柱 円柱 角錐 円錐 球 A 教遊者 |
 立体の体積まとめ 角柱 円柱 角錐 円錐 球 A 教遊者 |  立体の体積まとめ 角柱 円柱 角錐 円錐 球 A 教遊者 | 立体の体積まとめ 角柱 円柱 角錐 円錐 球 A 教遊者 |
立体の体積まとめ 角柱 円柱 角錐 円錐 球 A 教遊者 |  立体の体積まとめ 角柱 円柱 角錐 円錐 球 A 教遊者 |  立体の体積まとめ 角柱 円柱 角錐 円錐 球 A 教遊者 |
「立体 面積」の画像ギャラリー、詳細は各画像をクリックしてください。
 立体の体積まとめ 角柱 円柱 角錐 円錐 球 A 教遊者 |  立体の体積まとめ 角柱 円柱 角錐 円錐 球 A 教遊者 |  立体の体積まとめ 角柱 円柱 角錐 円錐 球 A 教遊者 |
 立体の体積まとめ 角柱 円柱 角錐 円錐 球 A 教遊者 |  立体の体積まとめ 角柱 円柱 角錐 円錐 球 A 教遊者 | 立体の体積まとめ 角柱 円柱 角錐 円錐 球 A 教遊者 |
 立体の体積まとめ 角柱 円柱 角錐 円錐 球 A 教遊者 |  立体の体積まとめ 角柱 円柱 角錐 円錐 球 A 教遊者 |  立体の体積まとめ 角柱 円柱 角錐 円錐 球 A 教遊者 |
「立体 面積」の画像ギャラリー、詳細は各画像をクリックしてください。
立体の体積まとめ 角柱 円柱 角錐 円錐 球 A 教遊者 | 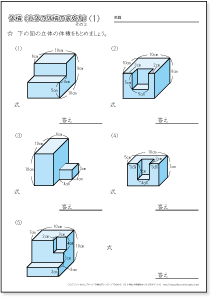 立体の体積まとめ 角柱 円柱 角錐 円錐 球 A 教遊者 |  立体の体積まとめ 角柱 円柱 角錐 円錐 球 A 教遊者 |
 立体の体積まとめ 角柱 円柱 角錐 円錐 球 A 教遊者 |  立体の体積まとめ 角柱 円柱 角錐 円錐 球 A 教遊者 |  立体の体積まとめ 角柱 円柱 角錐 円錐 球 A 教遊者 |
 立体の体積まとめ 角柱 円柱 角錐 円錐 球 A 教遊者 |  立体の体積まとめ 角柱 円柱 角錐 円錐 球 A 教遊者 | 立体の体積まとめ 角柱 円柱 角錐 円錐 球 A 教遊者 |
「立体 面積」の画像ギャラリー、詳細は各画像をクリックしてください。
 立体の体積まとめ 角柱 円柱 角錐 円錐 球 A 教遊者 | 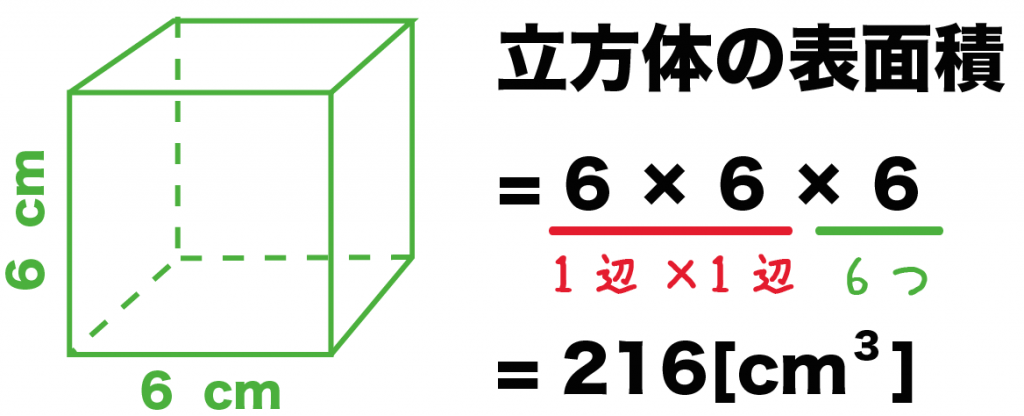 立体の体積まとめ 角柱 円柱 角錐 円錐 球 A 教遊者 |  立体の体積まとめ 角柱 円柱 角錐 円錐 球 A 教遊者 |
 立体の体積まとめ 角柱 円柱 角錐 円錐 球 A 教遊者 |  立体の体積まとめ 角柱 円柱 角錐 円錐 球 A 教遊者 |  立体の体積まとめ 角柱 円柱 角錐 円錐 球 A 教遊者 |
 立体の体積まとめ 角柱 円柱 角錐 円錐 球 A 教遊者 | 立体の体積まとめ 角柱 円柱 角錐 円錐 球 A 教遊者 | 立体の体積まとめ 角柱 円柱 角錐 円錐 球 A 教遊者 |
「立体 面積」の画像ギャラリー、詳細は各画像をクリックしてください。
立体の体積まとめ 角柱 円柱 角錐 円錐 球 A 教遊者 |  立体の体積まとめ 角柱 円柱 角錐 円錐 球 A 教遊者 |  立体の体積まとめ 角柱 円柱 角錐 円錐 球 A 教遊者 |
 立体の体積まとめ 角柱 円柱 角錐 円錐 球 A 教遊者 | 立体の体積まとめ 角柱 円柱 角錐 円錐 球 A 教遊者 | 立体の体積まとめ 角柱 円柱 角錐 円錐 球 A 教遊者 |
 立体の体積まとめ 角柱 円柱 角錐 円錐 球 A 教遊者 |  立体の体積まとめ 角柱 円柱 角錐 円錐 球 A 教遊者 | 立体の体積まとめ 角柱 円柱 角錐 円錐 球 A 教遊者 |
「立体 面積」の画像ギャラリー、詳細は各画像をクリックしてください。
 立体の体積まとめ 角柱 円柱 角錐 円錐 球 A 教遊者 |  立体の体積まとめ 角柱 円柱 角錐 円錐 球 A 教遊者 | 立体の体積まとめ 角柱 円柱 角錐 円錐 球 A 教遊者 |
立体の体積まとめ 角柱 円柱 角錐 円錐 球 A 教遊者 |  立体の体積まとめ 角柱 円柱 角錐 円錐 球 A 教遊者 | 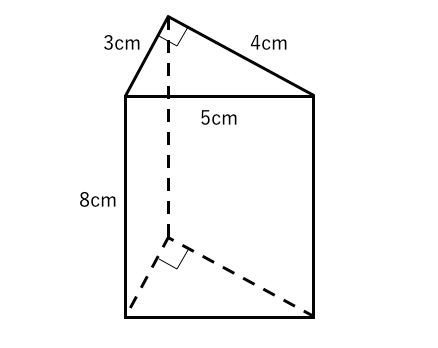 立体の体積まとめ 角柱 円柱 角錐 円錐 球 A 教遊者 |
 立体の体積まとめ 角柱 円柱 角錐 円錐 球 A 教遊者 | 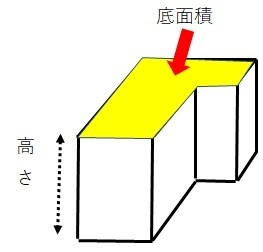 立体の体積まとめ 角柱 円柱 角錐 円錐 球 A 教遊者 |  立体の体積まとめ 角柱 円柱 角錐 円錐 球 A 教遊者 |
「立体 面積」の画像ギャラリー、詳細は各画像をクリックしてください。
立体の体積まとめ 角柱 円柱 角錐 円錐 球 A 教遊者 | 立体の体積まとめ 角柱 円柱 角錐 円錐 球 A 教遊者 |  立体の体積まとめ 角柱 円柱 角錐 円錐 球 A 教遊者 |
 立体の体積まとめ 角柱 円柱 角錐 円錐 球 A 教遊者 | 立体の体積まとめ 角柱 円柱 角錐 円錐 球 A 教遊者 |
底面積は S = 4 h 2 S=4h^2 S = 4 h 2 高さは h h h また,一辺 2 h 2h 2 h の立方体から同じ形の立体が六個取り出せるので,体積は (2 h) 3 ÷ 6 = 4 3 h 3 (2h)^3\div 6=\dfrac{4}{3}h^3 (2 h) 3 ÷ 6 = 3 4 h 3 以上より, V = 1 3 S h V=\dfrac{1}{3}Sh V = 3 1 S h が分かる。 表面積を求める問題は、展開図のまま計算した方が簡単に解けますね。 解答 (1) 三角錐 \(\mathrm{A−ECF}\) の立体図形は次のようになる。
コメント
コメントを投稿